Suman Chakravorty concentrates on Estimation and Stochastic Control of systems. His Estimation, Decision and Planning Laboratory is concerned with solving the many problems of Robotics and Situational Awareness posed by the challenges of the industry.
One of his recent projects involves motion planning under uncertainty via feedback-based information roadmaps (FIRM). This consists of an improved Simultaneous Localization and Mapping Method (SLAM) that includes replanning based on feedback that does not correspond to previous positions (sudden relocation of robot, misplaced or stolen). The following video shows a hardware implementation of this planning system:
Dr. Chakravorty also researches and implements techniques in Stochastical Dynamical Systems and Nonlinear Filtering. In this work , they pursue the problem of uncertainty propagation in complex nonlinear dynamical systems, specifically through the design of robust computational methods for the solution of the Fokker-Planck-Kolmogorov Equation. The Fokker-Planck-Kolmogorov equation is at
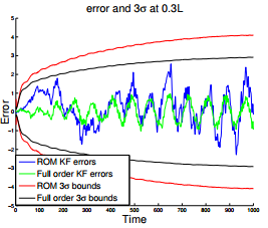
the core of any stochastic analysis and design problem. Specific applications of these methods are to the control of morphing wing aircraft and to the Air Traffic Control problem. Dr. Chakravorty and his group also pursue research on nonlinear filtering, in particular, we are very interested in the problem of space situational awareness and how advanced nonlinear filtering techniques based on the FPK equation can be applied to this problem. We are also very interested in the nonlinear filtering of very high dimensional systems, for instance, systems governed by PDEs as opposed to ODEs, that routinely have states in the order of millions. Such problems pose very unique and difficult challenges to conventional nonlinear filtering techniques such as the Kalman Filter. This work is at the intersection of this broad research thrust and that of robotic mapping and planning above.
For more information on Stochastical Dynamical Systems, Filtering and Planning under Uncertainty please visit: edplab.org.